PI Makes Untying Molecular Knots Possible
To gain a better understanding of DNA in a cell nucleus or in the Spike proteins of the SARS-CoV2 virus, we need to know how these molecules 'are wrapped', as well as the forces required to release certain molecular knots, also known as tertiary and quaternary molecular structures. To do this, researchers do exactly what we think they do: they pull on a thread-shaped end of the protein and measure the force necessary to release the twist or knot.
At this year's 'Single Molecule Biophysics Conference', Dr. Thomas Bocher, Director Segment Marketing - Global & Segment Marketing Manager ‘Microscopy & Life Sciences,’ spoke with a long-standing PI customer and top researcher in this area, Dr. David Dulin. For many years, David has been researching in the field of magnetic tweezers and is currently working as a professor at the Vrije Unversiteit Amsterdam (VU Amsterdam).
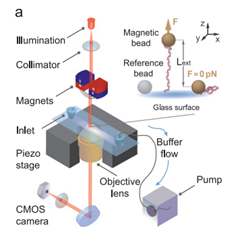
Similar to the related optical tweezers technology, magnetic tweezers require an optical microscope as an observational basis. David describes the measurement process in the following way, a fluorescent, paramagnetic, extremely small bead is attached to the top end of the molecule. The lower end of the molecule is attached to the glass plate of the microscope slide. A height-adjustable and rotatable magnet hangs over this and pulls the magnetic bead and, hence, the molecule upwards. An inverse microscope observes the position and height of the fluorescent bead (from below). For all of the important steps in this experiment, PI is a strong partner for David, as PI provides the M-126.PD1 for vertical movement, and the C-150.PD for the magnet's rotary movement, both with Mercury controllers. A PIFOC P-726 with E-753 controller is used to focus the microscope's objective lens for observation of the fluorescent magnetic bead.
But how do we measure the force necessary to straighten out a molecule that is twisted into a spiral shape, or the force required to untie a knot? This is where physics comes in. This is because to measure the force required, with the help of the microscope and automatic image processing, we must study the Brownian fluctuation of the magnetic bead's movement, which varies depending on the force applied. To put it more precisely, we apply the fluctuation-dissipation theorem (FDT) with calculations in the Fourier space. The result of the calculation is the applied force which, as expected, is extremely small and typically lies between 50fN (Femto Newton) and 60pN (Pico Newton).
Researchers already frequently duplicate the magnetic tweezers systems, similarly to the related optical tweezer technology which already has commercial manufacturers who are amongst PI's customers. In the future, this will lead to many more orders for PI.
Contact person: Dr. Thomas Bocher, Director Segment Marketing - Global